[BOJ, 백준] 10844 - 쉬운 계단 수 (C++)

https://www.acmicpc.net/problem/10844

문제

45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

입력

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

출력

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

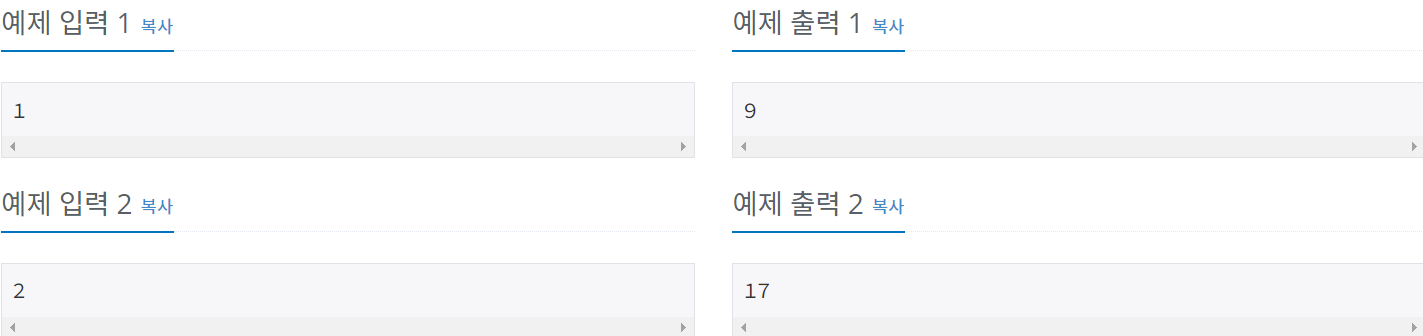
예제 입출력

풀이

#include <bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin >> n;
    long long dp[1001][10];
    dp[0][0]=0;
    for (int i=1; i<10;i++)
        dp[0][i]=1;
    for (int i=1; i<1000;i++){
        for (int j=0;j<10;j++){
            if (j==0) dp[i][j]=dp[i-1][j+1]% 1000000000;
            else if (j==9) dp[i][j]=dp[i-1][j-1]% 1000000000;
            else dp[i][j]=(dp[i-1][j+1]+dp[i-1][j-1])% 1000000000;
        }
    }
    long long ans=0;
    for(int i=0; i<10;i++) ans+=dp[n-1][i];
    cout << ans%1000000000;
}

문제 예시가 너무 적어서 맞는 답인지 확인하기 좀 어려운 문제였다.

만약 n=1일 때를 생각하면 계단수는

1 2 3 4 5 6 7 8 9

로 총 9가지이다. 그리고 n=2일 때를 생각하면

10 12
21 23
32 34
43 45
54 56
65 67
76 78
87 89
98

이렇게 17개가 나오는 것을 알 수 있다. 여기서 끝의 자리가 중요하다는 것을 알 수 있다.

만약 n일 때 끝이 a인 수의 개수를 구하면 n-1일 때 끝이 a-1과 a+1인 수의 합이다. 하지만 끝이 0인 수의 개수를 구하면 n-1일 때 끝이 1인 개수 인 것이다. 또한 끝의 자리수가 9인 수의 개수는 n-1일 때 끝이 8인 개수이다. 끝이 0일 때와 9일 때를 예외처리해서 구해주면 된다.

표로 나타내보면

n	1	2	3	4
0	0	1	1	3
1	1	1	3	4
2	1	2	3	6
3	1	2	3	7
4	1	2	4	7
5	1	2	4	7
6	1	2	4	8
7	1	2	4	8
8	1	2	4	7
9	1	1	3	4

위와 같이 되는 것이다.
답을 구할 때 prev(이전 값)와 now(현재 값) 두 개만 필요해서 dp배열을 저렇게 선언할 필요는 없었지만 그냥 생각 안나서 저렇게 했다.
그리고 ans에 꼭 % 1e9를 해줘야한다. 안해줘가지고 계속 틀렸었다.

알고리즘 분류: 다이나믹 프로그래밍